GSM-Technik, Seite zwo

Vorherige GSM-Technikseite

Sprachcodierung

Prinzipielle Anforderungen: Pflicht...

Der GSM-Sprachcodec (="Codierer/Decodierer") stellte technisch eine absolute Herausforderung dar: Die zur Verfügung stehende Bandbreite für die Sprachübertragung war recht gering, die Fehleranfälligkeit auf dem Übertragungsweg "Luft" aber bekannterweise sehr hoch.

Ähnlich wie im Computerbereich (Stichwort: JPEG- und MPEG-Komprimierung) war deshalb von Anfang an klar, daß die Sprachübertragung nur verlustbehaftet erfolgen könnte, d.h.: Die zum Einsatz kommenden Algorithmen müssen irrelevante Sprachanteile erkennen und weglassen. Aufgrund der unvermeidbaren Bitfehler auf der Luftschnittstelle sollte der (De-)Komprimierungsalgorithmus aber zusätzlich auch dann noch ein annehmbares Sprachsignal auf der Empfangsseite erzeugen können, wenn einzelne Bits verfälscht werden -ja sogar dann, wenn einzelne Datenpakete komplett ausfallen, denn aufgrund der Echtzeitübertragung hat das System ja keine Möglichkeit, als verfälscht erkannte Datenpakete neu anzufordern.

Außerdem war es schwierig, entsprechende Algorithmen zu bewerten, denn es gab und gibt keine geeignete Meßmethode, um die vom menschlichen Ohr wahrgenommene Sprachqualität objektiv zu bewerten, d.h.: Es waren aufwendige Hörtests nötig.

In salomonischer Lösung ist der 1987 von der GSM-Gruppe der CEPT gewählte Algorithmus deshalb auch die Kombination zweier Kandidaten mit drei Verfahren:

• Die Linear Predictive Coding (LPC) Technik und
• Die Long Term Prediction (LTP) Prädiktionstechnik und Regular Pulse Excitation (RPE)

,zusammen: RPE/LTP-LPC (eine Abkürzung, für die man eigentlich selbst schon eine Abkürzung bräuchte...)

...und Kür: DTX, VAD, CN Als wäre das ganze Verfahren der Sprachcodierung und -decodierung nicht allein schon kompliziert genug, wurde der Sprachcodec 1988 und 1989 nochmals erweitert: Eine höchstkomplizierte Sprechpausenerkennung (Voice Activity Detection, VAD) versucht, Sprechpausen zu erkennen und die Datenübertragung für diesen Zeitraum abzuschalten (Discontinous Transmission (DTX)).

Stattdessen wird auf der Empfangsseite ein möglichst passendes Hintergrundgeräusch simuliert (Comfort Noise (CN)), damit der Kunde nicht von der "digitalen Stille" irritiert wird...

Wozu dann überhaupt DTX? Nun, (zumindest zivilisierte) Menschen lassen einander aussprechen, d.h.: Bei einem normalen Gespräch werden allein dadurch schon ca. 50% der (Duplex-)Bandbreite einer Verbindung nicht ausgenutzt.
Rechnet man die Sprachpausen zwischen den einzelnen Wörtern und Sätzen mit, so liegt die theoretisch einsparbare Netzkapazität bei ca. 60% (!)
Da die VAD im Zweifel zugunsten einer Datenübertragung entscheiden muß und die Erkennung einer "Sprachpause" gelinde gesagt sauschwer ist, liegt das tatsächliche Einsparungspotential in der Praxis nicht ganz so hoch, beträgt aber immerhin noch ca. 35..45%.
Ähnliches gilt natürlich auch für den Energieverbrauch des Handys (es sendet in der Zeit ja nicht), allerdings geht ein Teil der hier eingesparten Energie wieder für den zusätzlichen Berechnungsaufwand für die Sprachpausenerkennung drauf.

Vorrangiges Ziel der Sprachcodierung war somit, auf der Empfangsseite eine subjektiv bestmögliche Reproduktion des Sprachsignals zu erreichen -was eben nicht unbedingt gleichbedeutend zu "möglichst bitgenaue Wiedergabe" sein muß: Darum wird in GSM-Netzen auch pingelig zwischen der Übertragung von Sprache und Daten (FAX, Email, etc.) unterschieden!

Der CODEC: RPE/LTP-LPC -oder: Von 64kbps zu 13kbps Genug des Vorgeplänkels:

Wie man dem Schaubild entnimmt, wird die Sprache zunächst digitalisiert. Nach dem auch hier gültigen Abtasttheorem muß die Abtastfrequenz mind. das zweifache der Signalbandbreite betragen; da die wichtigsten Sprachanteile der menschlichen Stimme in einem Bereich von knapp 4kHz liegen, wurde eine Abtastrate von 8000 Hz gewählt (zum Vergleich: Das normale Telefonnetz der Telekom überträgt nur den Frequenzbereich von 300..3400Hz).
Die Auflösung eines jeden solchen Abtastpunktes beträgt in der Regel 8 Bit (pseudologarithmische Quantisierung via A-Law gemäß CCITT G.711), manchmal aber auch 13 Bit (lineare Umsetzung, Zweierkomplement-codiert).
Jedenfalls ist der sich daraus ergebende Datenstrom von 8000*8 bzw. 8000*13 Bits pro Sekunde viel zu hoch.

Der CODEC: RPE/LTP-LPC -oder: Von 64kbps zu 13kbps

Wie macht man das? Eine alte Regel aller datenquetschenden Informatiker lautet: Je mehr Du über Deine Daten weißt, desto besser kannst Du Sie komprimieren!
Ein Beispiel: Angenommen, man wüßte, daß nur Klaviermusik übertragen würde. Dann genügte es, auf beiden Seiten ein Klavier (in Handyformat?...) vorzusehen; ein Algorithmus müßte dann "nur" (ähem...) die Noten und deren Spielweise senderseitig erkennen.
Auf der Leitung würde dann nicht die Musik selbst übertragen, sondern nur noch abstraktere Information, wie "spiele einen Dominant-Sept-Akkord in c-moll" und einige zusätzliche Parameter ("andante", "3/4-Takt" und all die anderen Scheußlichkeiten, mit denen man uns seinerzeit im Musikunterricht getriezt hat...).

Nach einem ähnlichen Prinzip funktioniert das GSM-Verfahren auch, nur wird hier eben nicht Klaviermusik, sondern menschliche Sprache übertragen. Das heißt:
Ein Modell der Erzeugung menschlicher Sprache muß her! Die dafür verwendeten Modelle zerlegen die Sprache nahezu alle nach dem gleichen Muster:

• Eine Stufe "entzieht" dem zu codierenden Sprachsignal einen quasi-periodischen Signalanteil, welches für die Formung stimmhafter Anteile (Vokale, Nasale) wichtig ist
• In weiteren Schritten wird das Restsignal geeignet übertragen

Die erste Stufe bestimmt nun einen bestmöglichen Filterparametersatz, wobei zwar auch Sprachinformationen benachbarter Sprachblöcke mitwirken, aber nur sehr begrenzt ("Gedächtnis" nur ca. 1ms). Der Schwerpunkt liegt bei der LPC-Stufe darin, die "Grobstruktur" des Signals zu übertragen und damit das zu übertragende Amplitudenspektrum schon einmal kräftig zu bereinigen.

Das an die LTP-Stufe übergebene Signal wird nun ähnlich gefiltert, allerdings berücksichtigt dieses "Langzeit-Prädiktions-Filter" (20ms sind nun mal computerseitig betrachtet "lange"...) dabei hauptsächlich längerdauernde statistische Abhängigkeiten der menschlichen Sprache (Silben, Lautbildung) und kann dadurch in der menschlichen Stimme auftretende periodische Signalanteile effektiv erfassen.
Auch diese gewonnenen Parameter werden übertragen, das damit empfängerseitig generierbare Näherungssignal vom Ursprungssignal abgezogen und der RPE-Stufe übergeben.

Dieses Restsignal hat nun bereits eine deutlich reduzierte Dynamik (d.h.: Das Amplitudenspektrum ist sehr flach, periodische Anteile nur noch gering ausgeprägt).
Anders gesagt bedeutet dies, daß die "wichtigsten" Sprachanteile schon durch die vorherigen Stufen erfaßt wurden. Die RPE-Stufe darf deshalb nun etwas weniger zimperlich sein und eine verlustbehaftete Codierung durch das Weglassen subjektiv irrelevanter Sprachinformation des Restsignals durchführen.

Aufgrund der geringen Dynamik des Restsignals erlaubt sich die Stufe zunächst eine Tiefpaßfilterung und anschließende Neuabtastung des Signals mit nur noch 1.3kHz (ca. 1/3 der ursprünglichen Abtastrate).
Genaugenommen zerlegt der Algorithmus das Signal in drei Signalfolgen (eine, welche den 1.,4.,7.,10.,.. Wert enthält, eine den 2.,5.,8.,11.,.. und einen den 3.,6.,9.,12.,..; die am besten "passende" dieser drei Folgen wird dann als Restsignal verwendet).

Im zweiten Schritt wird das übriggebliebene Restsignal in einem sog. "Kurzzeit-Prädiktions-Filter" auf statistische Abhängigkeiten benachbarter Abtastwerte untersucht und wieder daraufhin optimierte Parametersätze berechnet.

...und weiter zu 6.5kbps: Die Halfrate-Channels Auch die (momentan noch nicht eingesetzte) Halfratechannel-Technik setzt ähnliche CELP-Komprimierungstechnik ein, darf aber bis zu 4x soviel Rechenpower dazu verwenden, um im Ergebnis die benötigte Übertragungsbandbreite zu halbieren. Da letztlich nur noch halb soviele Bits übertragen werden, werden die Bedingungen aber auch bei der Fehleranfälligkeit ungemein härter: Der Ausfall einzelner Bits bei der Übertragung wiegt schwerer und die Informationen eines Sprachblocks lassen sich auch nur mehr über 4 statt 8 Datenpakete verteilen (Bit-Interleaving, s.u.).
Auf der Luftschnittstelle ist deshalb der Anteil der eingefügten Redundanzbits erheblich höher: 6.5kbps Informationen werden mit insgesamt 11.4kbps Datenrate übertragen (zum Vergleich: 13kbps zu 22.8kbps beim normalen Fullrate-Channel).

Fehlerschutzmechanismen Die Datenübertragung per Funk ist um einige Zehnerpotenzen fehleranfälliger als die kabelgebundene, so daß es nicht verwundert, daß bei GSM-Systemen ein erheblicher Aufwand zur Sicherung der Daten gegen Übertragungsfehler betrieben wird.
Zum einen wird dazu die gerade eben erst durch die Sprachcodierung mühsam verringerte Bandbreite durch Hinzufügen von Redundanz und Prüfsummen wieder auf 22.8kbps (bzw. 11.4kbps beim Halfratechannel) erhöht, zum anderen werden aber auch raffinierte Übertragungstricks angewendet.

1. Redundanzerhöhung:
   Im GSM-System werden die Daten wie bereits erwähnt in 20ms-Blöcken übertragen. Bei einer Nutzdatenrate von 13kbps entspricht dies also zunächst 260 Bit großen Datenpaketen.
   Diese werden nun schrittweise auf 456 Bits ergänzt (=22.8kbps):

   • Umordnen: Die Daten werden gemäß ihrer Wichtigkeit in 3 Klassen aufgeteilt:
     50 sehr wichtige Bits + 132 wichtige Bits + 78 weniger wichtige Bits

   • Prüfsumme: Für die als wichtigsten eingestuften Bits wird eine CRC-Summe (3 Bit) berechnet (für die Freaks: Das zugehörige Generatorpolynom lautet g(n):=n^3+n+1):
     
     
     

   • Erweiterung und erneute Umordnung: An die "wichtigen" Klasse1- und Klasse1a-Bits werden nun 4 sogenannte Tailbits "0000" angehängt. Ohne groß auf die dahinterstehende Mathematik eingehen zu wollen: Diese auf den ersten Blick unsinnige Maßnahme erhöht nochmals den Schutz von Bits am Anfang und Ende der (53+132) Bitsequenz, so daß eine erneute Umordnung vorgenommen wird, bei der die wichtigsten Bits an den Rand dieses 185 Bitblocks versetzt werden:
     (53 Bits + 132 Bits + 4 Nullbits) + 78 Bits

   • Faltung: Die vorderen Bitblöcke mit den insgesamt 189 als "wichtig" klassifizierten Bits werden nun einem sog. "Faltungscodierer" unterzogen, der den Datenumfang letztlich durch Einfügung von Redundanz verdoppelt:
     378 Bits + 78 Bits = 456 Bits

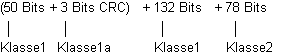
     Der verwendete Faltungscodierer ist dabei ein relativ einfach aufgebauter Baustein:
     
     
     

     Dieses Verfahren erlaubt im Mittel immerhin die Korrektur von ~25% aller Übertragungsfehler.

2. Übertragungstricks:
   Murphy's "Es kommt immer alles auf einmal!" gilt auch für Übertragungsfehler: Sie haben die Tendenz "en bloque" aufzutreten, d.h.: Sowohl zeitlich als auch frequenzmäßig gehäuft aufzutreten.
   Die GSM-Systeme versuchen deshalb, die zu übertragenden Daten über die Zeit und die Frequenz zu streuen, um die Auswirkungen von Blockfehlern so abzumildern, daß sie durch die Redundanz wieder korrigiert werden können:

   • Bit-Interleaving: Das Bit-Interleaving ("Verspreizung") verteilt die 456 Bits eines Sprachblocks über 8 Datenpakete, um Fehler über die Zeit (=mehrere Rahmen) zu streuen. Zusätzlich werden ursprünglich benachbarte Bits möglichst weit über die 8 Datenpakete verstreut, um somit auch die Zerstörung benachbarter Bits zu vermindern.
     (Für die GSM-Datendienste wird das Verfahren noch weiter getrieben: Hier werden die Bits auf bis zu 19 Pakete verteilt; das ist bei den Sprachdiensten jedoch nicht möglich, denn das empfängerseitige Zusammenklauben der verteilten Informationen bedeutet längere Wartezeiten, bis der Datenblock vorliegt und die so resultierende Verzögerung wäre für interaktive Sprache zu lang -wer schon mal über Satellit telefoniert hat, kennt den Effekt).

   • Frequency-Hopping: Zusätzlich werden die Informationen auch über das Frequenzspektrum gestreut, d.h.: Die einzelnen Datenpakete werden auf verschiedenen Trägerfrequenzen verschickt, so daß die Störung einer Frequenz weniger ins Gewicht fällt.

   • Extrapolation:
     "Na dann... ...versuchen Sie eben, möglichst gut zu schätzen, Mr. Spock!"
     --Captain Kirk
     
     Wenn all dies nichts nützt, dann kann sich sich das System auf der Empfangsseite noch mit einem aus der CD-Technik bekannten Trick aushelfen:
     Ist das empfangene Datenpaket nicht wiederherstellbar, so wird es schlicht ignoriert und stattdessen der Parametersatz des letzten Sprachrahmens verwendet. Technisch bewirkt dies eine Interpolation der Ausgangswerte, die subjektiv kaum bemerkbar ist. Erst nach 320ms kontinuierlich falschen Sprachrahmen wird der Ausgang komplett stumm geschaltet.

---

Modulationstechnik: GMSK

Betrachtet man das Handy als Black-Box (und das dürften die meisten normalerweise tun...), dann bleibt letztlich ein Datenstrom von 156.25 Bit alle 0.577 ms (=270833bps), der an irgendeinem Chip-Ausgang herauspurzelt und per Funk übertragen werden muß. Nun sind dies aber zunächst digitale Daten, die auf einem (200kHz breitem) analogen Frequenzkanal irgendwie gesendet werden müssen.

Für das "irgendwie" muß nun doch wieder die gute alte Analogtechnik herhalten: Man nehme eine analoge Grundfrequenz ("Träger") und packe durch gezielte Änderungen der Frequenz, der Lautstärke oder der Phase des Signals die Informationen auf diesen Träger. Dieses Verfahren namens Modulation ist von seinem Grundprinzip her eigentlich ein uralter Hut, allerdings hat die im GSM verwendete Variante namens Gaussian Minimum Shift Keying (GMSK) einige Finessen.

GMSK erlaubt es, den GSM-Datenstrom von 270833bps über einen Kanal von 200kHz Bandbreite zu übertragen. Der Knackpunkt bei der Datenübertragung ist, daß ein typisches Digitalsignal (0->1 oder 1->0) eigentlich senkrechte, d.h.: mathematisch unendlich steile Signalflanken fordert. Das dies in der Praxis Probleme bereitet, wird schon intuitiv klar: Kein real existierendes System kann "unendlich schnell" Zustandsübergänge bewerkstelligen. Ohne groß in die Mathematik der Fouriertransformationen einsteigen zu wollen, besteht mathematisch ein Zusammenhang zwischen der Bandbreite, die zur ordentlichen D/A-Wandlung eines Signals erforderlich ist und der Steilheit seiner Signalflanken. Aus diesem Grund wird das Rechtecksignal absichtlich "verschliffen" (Wen's interessiert: Dazu wird die Signalfunktion mathematisch gesehen mit der Gaußfunktion gefaltet, was einer Tiefpaßfilterung entspricht; die Übertragungsfunktion lautet
T(f)=e^{(-ln2/(2*B2) * f2)}, wobei B die 3dB-Bandbreite des Gaußtiefpasses darstellt; der GSM-Standard empfiehlt dabei Bandbreite*Bitrate=0.3).

(Dabei repräsentiert t/T die Zeit in Symboldauern).

Durch diese "Breite" der einzelnen Bits kommt es zu Signalüberlagerungen benachbarter Bitwerte. Außerdem streuen auch noch Störungen auf der Funkstrecke ein, so daß es auf Empfangsseite zu komplexen Signalmustern kommt, die erst wieder aufgelöst werden müssen.

Aus diesem eintreffenden Signalmix versucht der sog. Viterbialgorithmus nun, diejenige Datenfolge herauszuinterpretieren, die für den empfangenen Signalverlauf am wahrscheinlichsten ist -Keine leichte Aufgabe, denn da die Nutzdaten eines Bursts aus zwei 57 Bitblöcken besteht, gibt es immerhin 2^114 mögliche Kombinationen. Durch geschickte Analyse des Signalabbilds der (bekannten, da immer gleichen!) Trainingssequenz in den Bursts können jedoch Rückschlüsse auf die Art der Signalverfälschungen gezogen und die (unbekannten) Nutzdatenbits leichter gefunden werden. (Wieder etwas für die Freaks: Der Suchraum reduziert sich auf die Breite der Impulsantwort, bei 5 Bits also auf 2^5 Suchpfade).

Sicherheitsaspekte

Hinzukommt aber auch noch ein zweiter Punkt, den die Informatiker in Ihrem Fachchinesisch "Authentisierung" nennen: Dies beschreibt die Maßnahmen, die nötig sind, um sicherzustellen, daß derjenige, welcher ein Gespräch führt, auch wirklich der ist, der er zu sein vorgibt. (Derjenige, der behauptet, den letzten Schachtelsatz, der vor diesem Satz, der in dem Abschnitt der Datei, die Sie hier lesen, die über GSM-Sicherheitstechnik Auskunft gibt, vorkommt, steht, verstanden zu haben, zeigt, daß er deutsch kann... -so, ist der Stapel im Gehirn jetzt leer gepopt?).

Hierzu werden mehrere Mechanismen eingesetzt, die in recht komplizierter Weise miteinander zusammenarbeiten müssen. Das ganze System bedient sich dazu verschiedener Kryptographie-Algorithmen und elektronischer Schlüssel (also letztlich Nummern).

Da ist zunächst einmal die internationale Mobilteilnehmerkennung IMSI ("International Mobile Subscriber Identity"), eine bis zu 15 Ziffern lange Nummer, die vom Netzbetreiber der SIM-Karte fest zugeordnet wurde. Genaugenommen besteht sie aus einem Ländercodeteil, einer Netz- und einer Teilnehmerkennung, aber da Sie die Zahl eh niemals sehen werden, ist dies gar nicht weiter wichtig. Wichtig ist nur, daß die IMSI durch dieses Verfahren weltweit eindeutig ist und sozusagen Ihre internationale Erkennungsmarke darstellt. Eine Kopie davon existiert auch im HLR/VLR-Register bzw. im AUC.

Dann wäre da noch die Mobilgerätekennung IMEI ("International Mobile-Station Equipment Number") zu nennen, sozusagen das Gegenstück der IMSI, aber diesmal für das Gerät. (An dieser Stelle sieht man übrigens wieder sehr schön die GSM-typische Trennung zwischen Teilnehmer einerseits und dem von ihm verwendeten Gerät andererseits).
Und schließlich gibt es noch den "Individual Subscriber Authentication Key" Ki, ein bis zu 128 Bit langer, geheimer Schlüssel, der von der IMSI abhängt und wie diese nur im SIM und AUC.

Authentisierung:

Der Authentisierungsvorgang an sich ist ein klassisches Problem der Kryptographie: Sie haben zwei Teilnehmer A und B, die sich "irgendwie" über einen unsicheren Informationskanal gegenseitig davon überzeugen müssen, daß sie auch wirklich A und B sind. ("unsicher" heißt hierbei, daß die Strecke zwischen A und B beliebig abgehört und/oder verfälscht werden könnte). Es reicht nun nicht, daß A einfach seine IMSI an B übermittelt und B sie mit seiner Kopie vergleicht -in dem Fall bräuchte man ja nur A's IMSI einmal mitprotokollieren und fortan könnte sich jeder unbemerkt als A ausgeben (zumindest solange, bis dessen monatliche Telefonrechnung die Höhe des Empire State Buildings erreicht hat). Deshalb kommt ein algorithmisches Verfahren zum Einsatz, bei dem der Schlüssel selbst niemals über die Luftschnittstelle übertragen werden muß: Anstatt den Schlüssel zu schicken, sendet man Informationen, mit denen man nur testen kann, ob die Gegenseite ihn besitzt. Das ganze kann man sich vereinfacht so vorstellen, daß der Schlüssel als Teil einer Funktion benutzt wird: Im GSM heißt diese Funktion "A3"; genauer: A3 ist ein (für alle einheitlicher) Algorithmus, aber der Teilnehmerschlüssel parametrisiert diesen Algorithmus zu einer für den Teilnehmer einmaligen Funktion. Da außer A und B niemand sonst den Schlüssel kennt, ist damit auch diese spezielle teilnehmerspezifische A3()-Funktion nur A und B bekannt. Will sich B davon überzeugen, daß A den Schlüssel kennt, dann erzeugt B eine Zufallszahl RAND und teilt sie A mit: A berechnet A3(RAND) und schickt dieses Ergebnis (auch "signed response", SRES genannt) an B zurück. Da B die Funktion ja ebenfalls kennt, kann es A3(RAND) selber berechnen und mit A's zurückgeschicktem Wert vergleichen: Stimmen die beiden überein, dann kann B davon ausgehen, daß A im Besitz des Schlüssels ist. (RAND ist im GSM-Netz eine 128 Bit große Zahl, A3(RAND) ein 32 Bitwert).

Um das ganze noch ein Stückchen komplizierter zu machen, arbeiten Handy und MSC als konkrete Kommunikationspartner übrigens gar nicht auf der Basis der IMSI-Daten, sondern auf der sogenanten TMSI ("Temporary Mobile Subscriber Identity"), einer vom VLR generierten Teilnehmernummer mit ziemlich kurzem "Verfallsdatum", die z.T. noch während eines Gesprächs ausgewechselt werden kann.
Weiterhin muß die ganze oben beschriebene Authentisierungsprozedur in weniger als 0,5s abgeschlossen sein.

Verschlüsselung:

Während dieses Authentisierungsprozesses arbeitet noch eine andere Funktion, A8 genannt, nach demselben Schema: Ihr Ergebnis A8(RAND), ein 64 Bitwert, wird jedoch nicht über das Netz übertragen, sondern dient als sog. "Ciphering Key" Kc für die nun einsetzende Verschlüsselung aller Nutzdaten des Gesprächs.

Die Verschlüsselung der Nutzdaten erfolgt mit dem sog. A5-Algorithmus. Im Gegensatz zu den anderen Funktionen A3 und A8 ist er jedoch für alle GSM-Netze standardisiert.

• Die GSM-Empfehlungen - wo steht was?

Zurück zur ersten GSM-Technikseite
Zurück zu meiner Homepage
Zurück zur Mobilfunkstartseite