Übertragungsverfahren: FDMA, TDMA, CDMA

Alle Systeme, die Daten per Funk übertragen wollen, stehen vor dem selben Grundproblem: Das physikalische Übertragungsmedium existiert nur einmal; wollen mehrere Benutzer gleichzeitig kommunizieren, muß man deshalb geeignete Verfahren finden, um diesen Mehrfachzugriff zu organisieren.

Im Laufe der Geschichte wurden dazu drei Methoden entwickelt:

• FDMA (Frequency Division Multiple Access, Frequenzmultiplex)
• TDMA (Time Division Multiple Access, Zeitmultiplex)
• CDMA (Code Division Multiple Access, Codemultiplex)

In der Praxis findet man oftmals auch Mischformen dieser Systeme. So verwendet GSM beispielsweise ein kombiniertes FDMA/TDMA-Verfahren. Die nächste Mobilfunkgeneration UMTS wird zusätzlich auch noch CDMA einsetzen.

FDMA

Das FDMA-Verfahren ist sehr einfach zu verstehen: Interpretiert man das gesamte zur Verfügung stehende Frequenzband als die Ressource, welche es unter mehreren Benutzern aufzuteilen gilt, dann ist die simpleste Methode sicherlich die, jedem Benutzer einen bestimmten Anteil dieses Frequenzbandes zuzuordnen.
Wenn sich jede Datenübertragung auf den ihr zugeteilten Frequenzkanal beschränkt, so kollidieren die Übertragungen nicht gegenseitig.
Dieses Verfahren ist einfach, es hat aber auch einige Nachteile:

• Durch die festzugeordneten Frequenzkanäle wird auch dann Kapazität gebunden, wenn gerade kein oder nur wenig Verkehr auf den einzelnen Kanälen stattfindet
• Benachbarte Kanäle beeinflussen sich aufgrund physikalischer Effekte gegenseitig
• Störungen einzelner Frequenzen haben massiven Einfluß auf den betroffenen Kanal
• Verwendet man eine Instanz, welche die Gespräche über die zur Verfügung stehenden Kanäle verteilt ("frequency hopping", Frequenzsprungverfahren), so müssen die Geräte in der Lage sein, auf allen Frequenzkanälen des Spektrums zu senden bzw. zu empfangen

TDMA

Die zweite Methode, die einem sofort in den Sinn kommen sollte, besteht darin, daß man die Informationen nicht von den Frequenzen her staffelt, sondern in der zeitlichen Dimension unterteilt: Dazu gibt man sich ein Zeitraster vor und erlaubt jedem Teilnehmer nur in einem ihm zugeordneten Zeitfenster Daten zu übertragen.
(Dieser Ansatz ist auch das Grundprinzip jedes Bussystems digitaler Computer: Gib eine Taktfrequenz vor, erlaube Datenübertragungen nur in den sich daraus ergebenden Zeitschlitzen und organisiere das Gesamtsystem so, daß keine zwei Komponenten denselben Zeitschlitz verwenden wollen.)
Letztere Randbedingung ist auch einer der Nachteile dieses Zeitmultiplex-Verfahrens:

• Alle Teilnehmer des Funknetzes müssen sich auf den Systemtakt synchronisieren
• Störungen beeinflussen immer das gesamte TDMA-Signal
• Das Verfahren macht nur bei digitalen Datenübertragungen Sinn (was heute sicherlich keinen Nachteil mehr darstellt...)

warum CDMA?

Beide vorgenannten Systeme haben das Problem, Bandbreite für Übertragungen zu reservieren, unabhängig davon, ob diese aktuell verwendet wird oder nicht.
Außerdem sind TDMA- und FDMA-Verfahren lokal stark fehleranfällig: Wenn eine Störung auf einer bestimmten Frequenz (FDMA) oder zu einem bestimmten Zeitpunkt (TDMA) auftritt, wird die Übertragung massiv beeinträchtigt.
GSM versucht durch Kombination von TDMA und FDMA diese Effekte zu kompensieren: Die Datenpakete (TDMA) werden sehr klein gehalten, mit reichlich Zusatzinformationen versehen und die Datenbits eines logischen Pakets darüberhinaus über mehrere physikalische Datenpakete gestreut, so daß der Wegfall eines einzelnen Pakets meistens ausgeglichen werden kann. Außerdem werden die einzelnen Datenpakete mittels Frequenzsprungverfahren auf verschiedene Frequenzen (FDMA) verteilt, um auch den Einfluß von Störungen einzelner Frequenzen zu verringern.
Ein komplexer Algorithmus sorgt dann für die Verschachtelung der Informationen über die Frequenzen, Zeitschlitze und Datenpakete hinweg und verwaltet die Ressourcen auf der Luftschnittstelle, um Kollisionen durch Mehrfachbelegungen zu vermeiden.
Im Resultat erhielt man somit zwar ein recht verläßliches, dafür aber auch vergleichsweise aufwendiges System.

Die Frage stellte sich deshalb, ob man nicht vielleicht durch ein anderes Vielfachzugriffsverfahren ebenfalls die beschriebene Robustheit gegen Störungen realisieren könnte, das die entsprechenden Eigenschaften aber schon selbst mitbringt.

Schaut man sich nun nochmals am Beispiel von drei Datenkanälen genauer an, welche physikalischen Parameter man denn nun eigentlich bei den beiden gerade beschriebenen Verfahren variiert hat...

(Die Kanäle unterscheiden sich in ihren Frequenzen, können aber zur gleichen Zeit und mit gleicher Leistung senden)

(Die Kanäle benutzen dieselbe Frequenz (und Leistung), sind dafür aber in der Zeit disjunkt)

...so drängt sich eine dritte Variante auf ganz natürlich-naive Weise auf:

CDMA

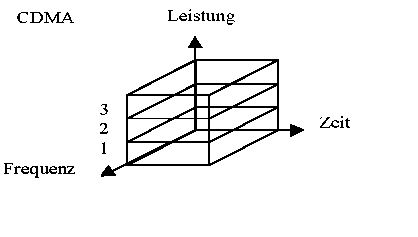
Analysiert man die beiden anderen Verfahren FDMA und TDMA nochmals daraufhin, warum es bei ihnen möglich ist, empfangsseitig die Daten selektiv eines gewünschten Kanals herauszufiltern, so wird man schnell fündig: Es existiert jeweils gemeinsames Wissen über den interessierenden Kanal (bei FDMA: Die dem Kanal zugeordnete Frequenz; bei TDMA: Die dem Kanal zugeordneten Zeitschlitze), mit denen das Signal von allen anderen unterschieden werden kann -die Kanäe sind durch diese Parameter "orthogonal" zueinander.

Geht man (sinnvollerweise) davon aus, daß sich die Sendestärken der einzelnen Kanäe nicht wesentlich voneinander unterscheiden, so bleibt nur die Art der Bitkodierung: Wenn die Bits schon im selben Spektrum zur selben Zeit und mit vergleichbarer Leistung abgestrahlt werden, dann muß eine logische "1" des einen Kanals eben anders aussehen als eine logische "1" eines anderen Kanals, um sie voneinander unterscheiden zu können!

Bits werden durch zeitabhängige Signalpegel, also mathematisch genauer: Übertragungsfunktionen gesendet; ergo müssen diese zur Bitkodierung verwendeten Übertragungsfunktionen zueinander "orthogonal" sein. -Was heißt das aber genau?

Wer sich noch finster an seine "Lineare Algebra"-Schulstunden zurückerinnern kann, dem fällt vielleicht hierzu das Skalarprodukt von Vektoren ein: Zwei Vektoren a, b werden miteinander multipliziert, indem man ihre Komponenten stellenweise miteinander multipliziert und die Ergebnisse aufsummiert:

Zwei Vektoren sind dann orthogonal zueinander, wenn dieses so gebildete Skalarprodukt a xb = 0 ist (kleiner Einwurf: Dieses Skalarprodukt hat natürlich noch eine umfassendere Bedeutung. Ist sein Wert 1, so sind die Vektoren bspw. zueinander parallel; allgemein gilt für den Winkel zwischen zwei Vektoren die Gleichung )

Damit hat man aber schon das Rüstzeug für eine orthogonale Kodierung der Daten beisammen: Verwendet man nämlich einen Satz zueinander orthogonaler Vektoren, ordnet jedem Vektor einen Datenkanal zu und interpretiert die Komponenten des Vektors als Signalstärken für die Übertragung eines Bits, dann kann man damit aus dem Summensignal aller Kanäle, wie es beim Empfänger ankommt, durch Skalarproduktbildung mit dem Vektor des gewünschten Kanals die Daten zurückgewinnen.

Ein Beispiel dazu für n=3: a=(0.5,0.5,w); b=(-w,w,0); c=(-0.5,-0.5,w), dabei stehe w abkürzend für wurzel(2)/2 = 0.707.... Wie man selber einfach nachprüfen kann, sind die drei Vektoren orthogonal: a x b = a x c = b x c = 0:


Eine logische "1" in einem Kanal wird dann dadurch übertragen, daß der dem Kanal zugeordnete Vektor v gesendet wird; eine logische "0" durch Übertragung des inversen Vektors -v und wird in dem Kanal momentan gar nichts gesendet, so entspricht dies der Übertragung des Nullvektors.

Nehmen wir nun an, im zu betrachtenden Augenblick wird im 1.Kanal "0" gesendet, im 2.Kanel "1" und im 3.Kanal gar nichts: Dies entspricht nach dem eben gesagten der Übertragung von -a, b und 0. Diese drei Signale überlagern sich, so daß ein Empfänger nur den Summenvektor s = -a+b+0 = (-0.5-w,-0.5+w,-w) sieht:

Will der Empfänger nun wissen, welche Signale in den drei Kanälen jeweils gesendet wurden, so reicht dazu eine einfache Skalarproduktbildung aus:

1. Kanal: a x s = (0.5,0.5,w) x (-0.5-w,-0.5+w,-w) = 0.5*(-0.5-w) + 0.5*(-0.5+w) + w*(-w) = -0.25-0.5w-0.25+0.5w-0.5 = -1, d.h.: Es wurde der inverse Vektor dieses Kanals -also eine logische "0"- übertragen
2. Kanal: b x s = (-w,w,0) x (-0.5-w,-0.5+w,-w) = -w*(-0.5-w) + w*(-0.5+w) + 0*(-w) = 0.5w+0.5-0.5w+0.5 = +1, d.h.: Es wurde der Vektor dieses Kanals -also eine logische "1"- übertragen
3. Kanal: c x s = (-0.5,-0.5,w) x (-0.5-w,-0.5+w,-w) = 0.25+0.5w+0.25-0.5w-0.5 = 0, d.h.: Es wurde kein Signal übertragen

Eine einfache Grundregel der linearen Algebra besagt, daß man in einem n-dimensionalem Vektorraum maximal n linear unabhängige (also "orthogonale") Vektoren finden kann:
In einem TDMA- oder FDMA-System wird man für n verschiedene Timeslots bzw. Frequenzen deshalb auch nie mehr als n Gespräche gleichzeitig übertragen können: Die 100% Trennung ("Orthogonalität") der einzelnen Kanäle ist hier ja gerade das Funktionsprinzip für eine erfolgreiche Übertragung.
Bei CDMA genügt dagegen eine "hinlänglich" gute Näherung der Orthogonalität: Werden mehr als n Signale gleichzeitig übertragen, so wird das Verfahren verrauscht und in obigem Beispiel mehr oder weniger leicht von +1, -1 und 0 verschiedene Werte liefern, die aber immer noch nahe an diesen Werten liegen und deshalb wahrscheinliche Zuordnungen zu den Einzelvektoren der Kanäe zulassen.
Mit steigender Anzahl der Teilnehmer gegenüber der Kanalanzahl n nimmt die Zahl der Fehlinterpretationen dann immer weiter zu: CDMA hat hier also im Gegensatz zu den beiden anderen Verfahren keine "harte" Grenze, sondern sackt nur in der Qualität je Kanal immer weiter ab.

Zurück zu meiner Homepage
Zurück zur Mobilfunkstartseite